How to Use Simple Math to
Find The Sharps and Flats
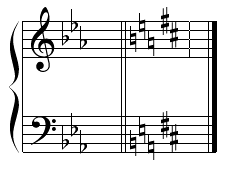
Key Signature Math is a fundamental principal that is used in creating a new key signature that adds one sharp at a time or one flat at a time.
Each key change that adds one new sharp is done by moving a perfect fifth from our current key signature root.
If we start with the key of C, where we have no sharps or flats, and move to the perfect fifth, which is G, it will add one sharp.
So what would be the new sharp?
How to Add Sharps and Change Keys
Let’s look at it a couple of different ways to apply Key Signature math.
The sharp will be defined by the major seventh interval which is 11 half steps from the key name, or the M7th of the scale.
The second way is to simple think of it as a half step down from the root note that is an octave above.
So for G it will be F#. The M7 or a half step down from G.
Look at how the scale is built for the G major scale. For review these concepts are covered in intervals and is expanded upon in the music theory of scales.
Interval: 1 2 3 4 5 6 M7 8
Scale steps: W + W + W + H + W + W + W + H
Notes: G - A - B - C - D - E - F# - G

The Major 7 (M7) is F#.
Review How the Key Signature Math Works for Sharps
- To obtain the next key signature that adds a sharp – it is called the name of the perfect fifth from where you started. ( C to G ),
- the sharp added was the major seventh interval of the new key, which is a half step down from the octave of the new key, (F# is the M7 or a half step down from G).
Considering Flats
The fundamental way to consider flats is actually a continuation of the sharps once you have added all seven sharps. It would involve changing all the sharps to flats and then reducing the flats one at a time.
You will see how that is done when we work with our circle of fifths in the next segment.
However, for building the flat keys there is another way of doing it if we start with the key of C and add one flat at a time. That involves using the idea of fifths and fourths again.
The first flat key will be the key of F it is a fifth down from C, (or alternately a fourth up from C) as shown on this keyboard.
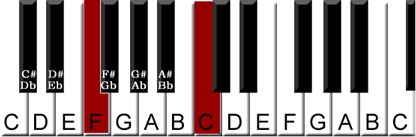
F Major Scale, by default has the Bb as the perfect fourth. That is our first flat.
Look at how the scale is built for the F major scale using the same formula as before:
Interval: 1 2 3 4 5 6 M7 8 Scale steps: W + W + W + H + W + W + W + H Notes: F- G - A - Bb - C - D - E - F
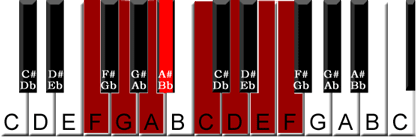
Review How the Key
Signature Math Works for Flats
-
To obtain the next flat key signature that adds a flat – it is called the name of the perfect fifth below where you started. ( C to F ),
-
The flat added was the perfect fourth interval of the new key, (Bb is the P4 from F).
Alternate Method of Math for Flats
-
Another way to look at it is the 4 + 4 method. If you look at the keyboard above and consider that if you started at C went a 4th up you are at F, the new key, another 4th and you have the Bb that is in the key.
- A pattern you will become familiar with is that the new flat to be added for the next key change will be a fifth down, just like the key. (or a fourth up)
Using the Math
In general you will use the fifths and fourths to develop the key signature math. So the next step is to take a bigger look at all the keys by developing this Circle of fifths.

